
Radioaktivität - Versuche
Wichtige Verhaltensweisen beim Umgang mit radioaktiven Materialen:
- Aufenthaltszeit verkürzen
- Abschirmung beachten
- Abstand wahren
- Tipp: Nicht mit den Fingern ins Gesicht fassen! – Aufgabe: Wieso sollte man sich nicht mit den Fingern ins Gesicht fassen?
- Tipp: Hand Wachen! – Aufgabe: Wieso ist das Händewaschen wichtig?
Nebelkammer:
Nachweis der Teilchenarten beim radioaktiven Zerfall durch eine Nebelkammer.

Abb. 1: Nebelkammeraufnahme [Mau2014]
Die radioaktiven Teilchen hinterlassen in der Nebelkammer weiße Spuren. Sind sie kurz und dick, so sind es meisten Alpha-Teilchen. Falls man ein Magnetfeld hinzuschaltet, kann man sowohl die Alpha-Teilchen als auch die Beta-Teilchen unterscheiden. Positronen und Elektronen weden auf Grund ihrer entgegengesetzten Ladung im Magnetfeld in entgegengesetzte Richtungen abgelenkt (Lorentzkraft). Alpha-Teilchen sind zweifach Positiv geladen, werden also im Magnetfeld ebenfalls abgelenkt.
Nebelkammer selbst bauen [HeiZimRie2015]
Video: Nebelkammer (Youtube)
Video: Nebelkammer II (Youtube) - Aufgabe: Sprache und Beschreibung kritisch anhören!
Versuch: Nullrate
Die Nullrate sollte über viele Messungen bestimmt werden. Es ergibt sich eine Verteilung der Messpunkte. Hierbei handelt es sich um eine Poisson-Verteilung. Im Gegensatz zur Normalverteilung handelt es sich um diskrete Werte.
Abb. 2: Verteilung von Kernzerfällen [Hei2015] – [Hei2015] Heinicke, S. (2015) Was ist denn jetzt das richtige Ergebnis? In: Heinicke, S. (Hg.) Radioaktivität. Naturwissenschaften im Unterricht Physik. 141/142 S. 38-43 Kritisieren Sie die Darstellungsweise des Grafen.
Versuch: Abstandsgesetzt:

Abb. 3: links - Abstandsmessung mit NTL; rechts Abstandsmessung mit CASSY - Aufgabe: Was wurde beim linken Aufbau nicht richtig gemacht?
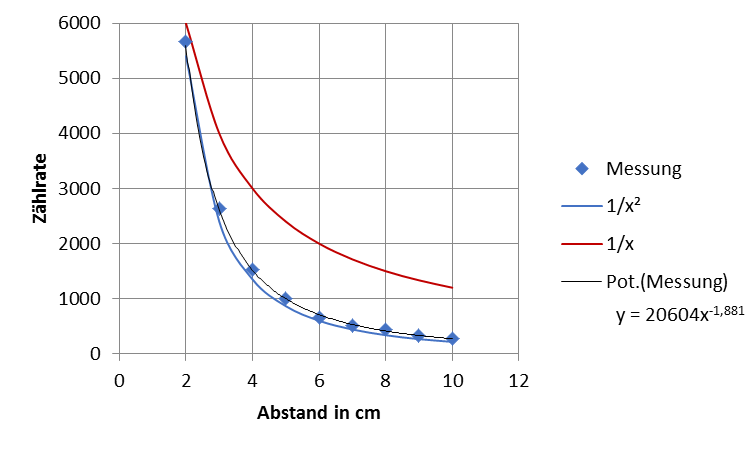
Die Anordnung wird wie auf Abbildung 3 angegeben aufgebaut. Das Papier schirmt die Alpha-Strahlung ab. Es ist also ein Gemisch aus Beta- und Gamma-Strahlung. In einer Tabelle wird die Zählrate für unterschiedliche Abstände aufgenommen. Da die Zerfälle statistisch verteilt sind, empfiehlt sich eine hohe Zählzeit (10 s oder 100 s). Die aufgenommenen Werte werden auf ein x-y-Diagramm übertragen. Mittels Exel wird ein Fitt versucht. Aufgabe: Welcher Fitt scheint gut zu passen, bzw. ist sinnvoll? Aufgabe: Linearisieren Sie die Messwerte. Wie sieht der Fitt aus?
 |
|
Abb. 4: Abstandsgesetz bei einer punktförmigen Strahlenquelle Tab.1 : Werte genomen aus [Vol1994a]
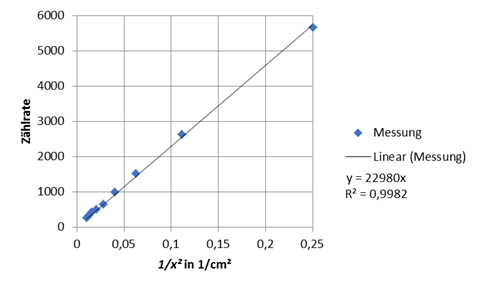
Überprüfen des 1/x² -Zusammenhangs durch Linearisierung.
 |
|
Abb. 5: Linearisiertes Abstandsgesetz bei einer punktförmigen Strahlenquelle Tab.2 : Umrechnung
Es ergibt sich eine Ursprungsgerade. Das Produkt aus Z und r² ist ähnlich.
Abschirmung:

Abb. 6: links - Abschirmungsmessung mit NTL; rechts Abschirmungsmessung mit CASSY - Aufgabe: Was wurde beim linken Aufbau nicht richtig gemacht?
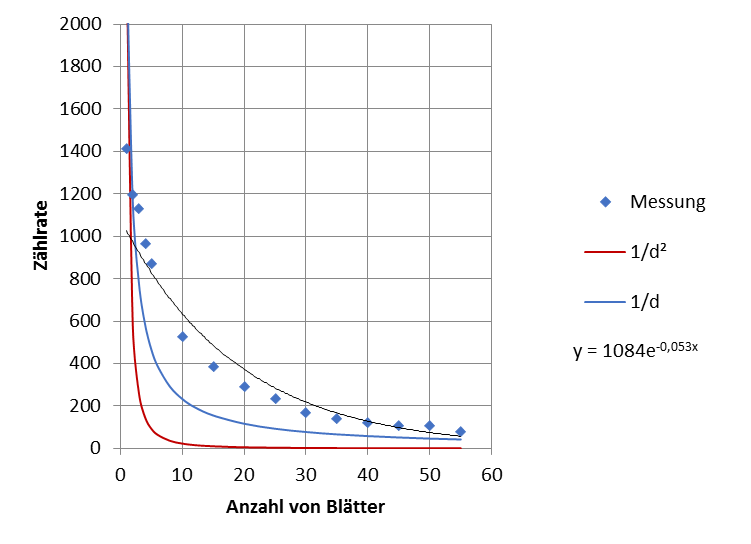
Die Anordnung wird wie in Abbildung 6 angegeben aufgebaut. Zwischen eine radioaktive Quelle und einem Zählrohr werden Papierblätter gehalten. Es ist also ein Gemisch aus Beta- und Gamma-Strahlung. In einer Tabelle wird die Zählrate für eine unterschiedliche Anzahl an Papierblättern aufgenommen. Da die Zerfälle statistisch verteilt sind, empfiehlt sich eine hohe Zählzeit (10 s oder 100 s). Die aufgenommenen Werte werden auf ein x-y-Diagramm übertragen.
 |
|
Abb. 7: Abhängigkeit von der Abschirmung Tab.3 : Werte genomen aus [Vol1994a])
Der Graf ist nicht gut anzufitten, da er aus verschiedenen Strahlungsarten besteht. Der eigentliche Zusammenhang sollte exponential sein. Außerdem sind die Probleme, die Exel beim Fitten macht gut zu sehen.Radioaktivitätsmessung mit dem Handy
Es ist möglich die Radioaktivität mit dem Handy zu messen. Hierfür braucht man ein App., wie z.B. RadioactivityCounter.
Die Linse (front oder back) muss abgeklebt werden (mit schwarzem Klebeband oder einer Aluminiumfolie), da die Kamera als Sensor fungiert.
Abb. 8: RadioactivityCounter (Apple Version)
Anwendung und Beschreibung: Kuhn, J. & Frübis, J. (2013) Smartphone als Geigerzähler. Phys. Unserer Zeit 5/2013 (44) p.253-255
Bierschaumzerfall
Der Bierschaumversuch eignet sich gut, um einen Zerfall zu beobachten. Er ist leicht durchführbar und - im Gegensatz zu den anderen Radioaktivitätsversuchen - ungefährlich.




Abb. 9: Bierschaumversuche Zylinder - Aufgabe: Was wurde bei den Bildern links schlecht fotografiert?
Es werden nur ein Zylinder (Abb. 9) mit Maßeinheit, Bier und eine Stoppuhr benötigt. In einer Tabelle werden zu bestimmten Zeiten sowohl der obere Wert (Schaumkrone), als auch der untere Wert (Übergang zwischen Schaum und Bier) aufgenommen. Hinweis: hier ist es leider so, dass man lange aufnehmen muss, da in der ersten Zeit der Schaum durch zwei Mechanismen zusammenfällt. Die Werte ab ca. 2 Minuten sind gut zum Aufnehmen.
Empfehlung: Nehmen Sie alkoholfreies Bier und befestigen Sie ein Maßband am Rand des Gefäßes, in das das Bier geschüttet wird. Als Stoppuhr kann auch ein Handy dienen.
| t in s | Erdinger h in cm | Augustiner h in cm | Budweiser h in cm |
| 0 | 17 | 14 | 14 |
| 15 | 16,1 | 11,8 | 12,1 |
| 30 | 14,9 | 10,5 | 10,9 |
| 45 | 14 | 9,3 | 10 |
| 60 | 13,2 | 8,5 | 9,3 |
| 75 | 12,5 | 7,7 | 8,6 |
| 90 | 11,9 | 7,1 | 8 |
| 105 | 11,2 | 6,5 | 7,5 |
| 120 | 10,7 | 6 | 7 |
| 150 | 9,7 | 5,3 | 6,2 |
| 180 | 8,9 | 4,4 | 5,5 |
| 210 | 8,3 | 3,5 | 4,5 |
| 240 | 7,5 | 2,9 | 3,5 |
| 300 | 6,3 | 1,3 | 2 |
| 360 | 5,2 | 0,7 | 0,9 |
Tab 2: Höhe des Bierschaums in Abhängigkeit der Zeit (Werte genommen aus [Lei2002])
Video: Rohlfing: Bierschaumzerfall (2016) (YouTube)
Aufgabe (aus Jugend und Volk, S.63, Übung 2.2.101):
Ein Glas Bier wird serviert. Der Bierschaum hat beim Servieren eine Höhe von 6 cm, nach 30 Sekunden hat die Höhe auf 5,5 cm abgenommen.
Aufgabenstellung:
Berechnen Sie unter der Annahme, dass die Höhe des Bierschaums exponentiell abnimmt, jenen Zeitpunkt, zu dem der Bierschaum nur mehr halb so hoch wie beim Servieren ist!
Lösung:
Video: Manuel Arslanyan: Bierschaum (exponentielle Abnahme berechnen) Jugend und Volk, S.63, Übung 2.2.101 (2016) (YouTube)
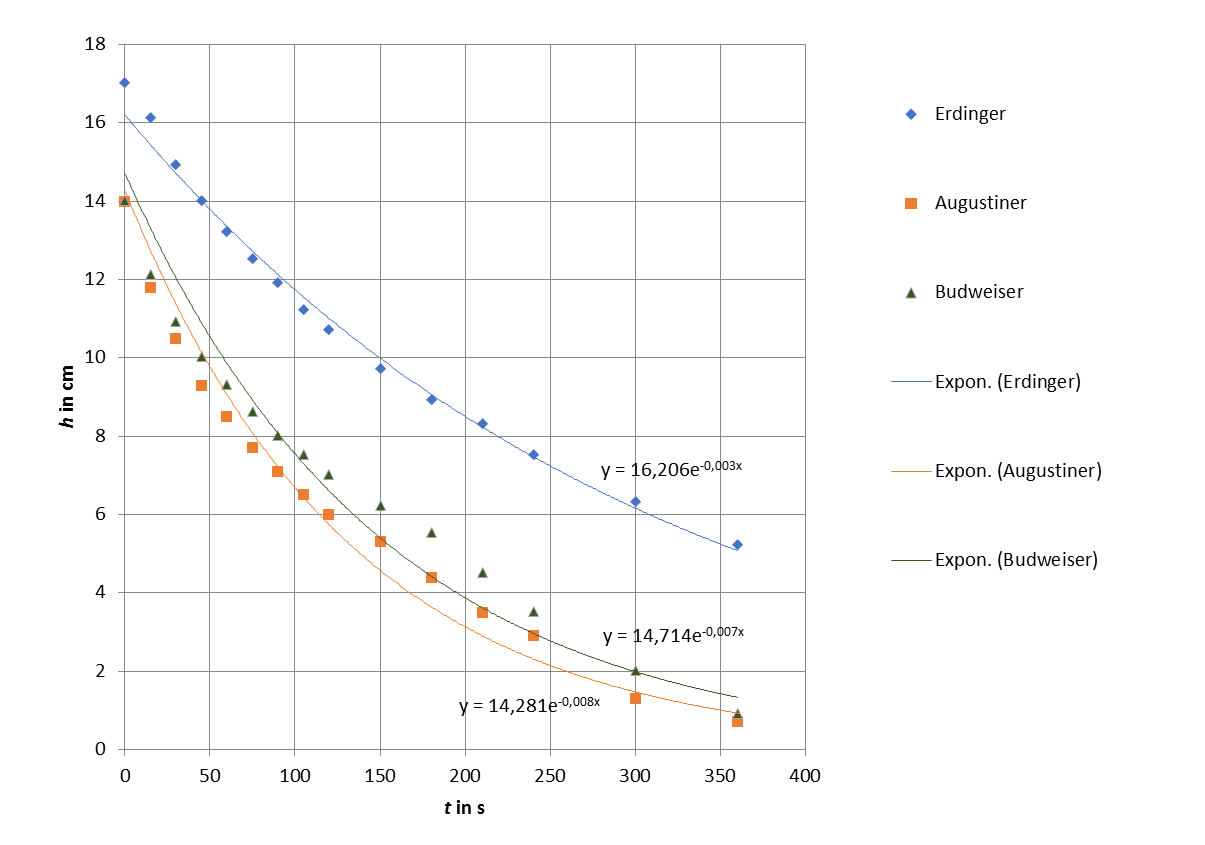
Abb. 10: Bierschaumzerfall gefittete Daten.
Natürlich Strahlungsquellen [Hag1994]:
Uran-238 Halbwertszeit 4,5·10^9 Jahre
Uran-235 Halbwertszeit 7,0·10^8 Jahre
Thorium-232 Halbwertszeit 1,4·10^10 Jahre
Kalium-40 Halbwertszeit 1,3·10^9 Jahre
Rubidium-87 Halbwertszeit 4,8·10^10 Jahre
ca. 16,4 mg K-40 pro Deutschen was einer Aktivität von 4256 Bq => mehr als 4000 Zerfälle pro Sekunde im Körper

Abb. 11: Jährliche Strahlenbelastung [BMI]
Versuch: Radioaktiver Staub
Das Radon-220 aus der Thoriumreihe und vor allem Ra-222 aus der Uranreihe bei der Belastung eine wichtige Rolle. Sie sind im Baumaterial enthalten und lassen sich nachweisen. Hierfür braucht man einen Staubsauer auf den ein Küchenpapier/Filter gespannt wird und eine kleine Öffnung (in etwa so groß wie das Detektorfenster) geklebt wird. Wichtig ist, dass der Raum in einem mindestens zwei Tage nicht gelüfteten Raum ohne Zug (gut geht ein Kellerraum), gesaugt wird. Nach ca. 10 Minuten hat man genügend Staub gesammelt um die Radioaktivität nachzuweisen. Außerdem kann (falls man genügend Zeit hat) der Zerfall gemessen werden (Am Anfang ist es kein exponentieller Zusammenhang). Man braucht aber mindestens 200 Minuten.
Abb. 12: Veränderung der Zählrate bei Hausstaub im Laufe von 200 Minuten nach Abschalten des Staubsaugers. [Hag1994]
Literatur
[HeiZimRie2015] Heinicke, S. Zimmermann, M. & Rieß, F. (2015) Dem Unsichtbaren auf der Spur. In: Heinicke, S. (Hg.) Radioaktivität. Naturwissenschaften im Unterricht Physik. 141/142 S. 38-43
[Lei2002] Leike, A. (2002) Demonstration of the exponential decay law using beer froth. In: European Journal of Physics. 23 (2002) 21-26
[Mau2014] Mauswiesel (2014) Picture taken at the Pic duMidi at 2877 m in a Phywe PJ45 diffusion cloud chamber. Size of the interaction surface if 45x45 cm. Von: Wikipedia: Cloud chamber
[Vol1994a] Volkmer, M. (1994) Untersuchung ionisierender Strahlen mit Papierfiltern. In: Unterricht Physik - Versuche zur Radioaktivität 1/94 Heft 21 März 1994
[Vol1994b] Volkmer, M. (1994) Untersuchung von Strahlenbündeln. In: Unterricht Physik - Versuche zur Radioaktivität 1/94 Heft 21 März 1994