Zeitdilatation
Wie bereits erwähnt war der Unterschied zu allen anderen Wissenschaftlern, dass Einstein mit diesen Erkenntnissen einfach weiterrechnete. Wir werden in den folgenden Rechnungen die Zeitdilatation herleiten, also dass die Zeit in einem bewegten Inertialsystem langsamer vergeht, aus Sicht eines außerstehenden Betrachters.
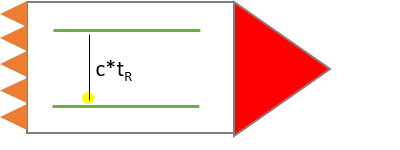
Dazu denken wir uns eine Lichtuhr, welche sich in einem Raumschiff befindet. Eine Lichtuhr besteht aus zwei Spiegeln und einem Sensor, welcher die Zeit misst, welche ein Lichtstrahl benötigt, um zwischen den beiden Spiegeln hin und her zu hüpfen. Das Raumschiff befindet sich zunächst in Ruhelage, also die Geschwindigkeitsdifferenz zum Beobachter auf der Erde ist 0. Da sich das Licht innerhalb der Lichtuhr immer mit der konstanten Geschwindigkeit v = 299 792 458 m/s (:=c) bewegt, lässt sich der Weg s (Entfernung Spiegel zu Spiegel) berechnen durch den Zusammenhang s=c*t.

Nun düst dieses Raumschiff mit einer Geschwindigkeit v relativ zur Erde an dem Beobachter auf der Erde vorbei. Aus Sicht des außenstehenden Beobachters muss das Licht nun einen längeren Weg zurücklegen, kann das aber nur mit maximal Lichtgeschwindigkeit tun. Nach dem Relativitätsprinzip hat sich für den Beobachter innerhalb des Inertialsystems in der Rakete nichts geändert. In einer Skizze sieht das aus Sicht der Erde in etwa so aus.

Die direkte Strecke vom Lichtpunkt am untern Spiegel zum Oberen ist c*tErde lang. Die horizontal zurückgelegte Strecke ist v*tErde lang.
Aus Sicht der Rakete hat sich nicht viel verändert unverändert. Die Strecke ist weiterhin c*tRakete lang.
Wir können die beiden Sachverhalte wie folgt zusammenführen:
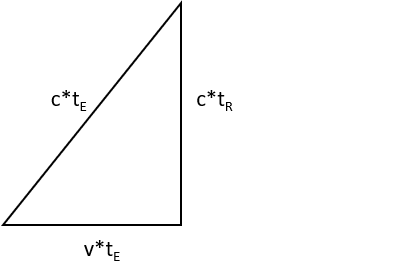
Die horizontale Strecke ist die Messung der Rakete mit der Zeit tR für Rakete. Damit ergibt sich für diese Strecke der Zusammenhang sy=c*tR. (sy aufgrund des Weges in Richtung der y-Achse).
Aus Sicht der Erde legt das Licht aber auch einen Weg in x-Richtung mit einer Geschwindigkeit v zurück, abhängig von der Geschwindigkeit der Rakete. So ergibt sich für den Weg in x-Richtung der Zusammenhang sx=v*tE und der resultierende Weg s=c*tE.
Aus dem Alltag würden wir vermuten, dass die Zeiten dieselben sein müssten. Hier aber unterscheiden sie sich voneinander, weshalb wir sie unterschiedlich benennen müssen.
Das Dreieck hat einen rechten Winkel, weshalb wir den Satz von Pythagoras anwenden können. Wir bekommen den Zusammenhang:
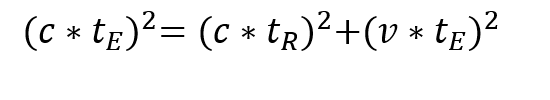
Durch geschicktes Umformen kommen wir schließlich auf die Formel:
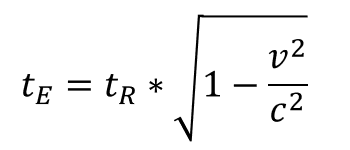
Mit tE bezeichneten wir die gemessene Zeit aus Sicht der Erde. Um diesen Begriff zu verallgemeinern schreiben wir ihn um in tBewegung und tR in tRuhe. Die eine Messung wird nämlich in Bewegung aus Sicht des einen Inertialsystems gemessen und die andere in Ruhe.
Damit erhalten wir die allgemeine Formel:
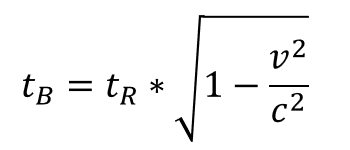
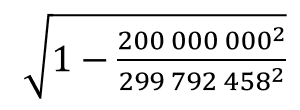
den Wert 0,677. Somit ist tE = tR * 0,677. Wenn wir also auf der Rakete 60 Sekunden stoppen, dann vergehen auf der Erde nur in etwa 40 Sekunden. Die bewegte Uhr ist also langsamer gelaufen.
Im Alltag tritt dieser Effekt auch auf, jedoch ist er dabei meist zu vernachlässigen. Wenn, wie im obigen Beispiel, ein Zug mit v=30 m/s relativ zum Beobachter vorbeifährt, dann ist der Wert 30/300.000.000 quasi Null und damit tBewegung fast gleich tRuhe.
Bei Satelliten hingegen ist dieser Effekt sehr real und würden diese nicht die Zeitdilatation einberechnen würde unser GPS heute nicht so gut funktionieren wie es das heute tut.
Schau dir dazu dieses Video an: https://www.youtube.com/watch?v=nLFJgqfjCA8&list=PLtChQtYYwX2PZeFpje0TsiCvXWCpIlBFj&index=4