Historische Atommodelle

 

Das Dalton-Modell

Nachdem bis in die Neuzeit keine Entdeckungen gemacht wurden, die in die Größenordnung von Atomen reichte, dauerte es bis 1803, als ein wegbereitendes Atommodell von John Dalton vorgestellt wurde. In seinem Modell gab es so viel verschiedene Atome, wie es Elemente gab. Dazu meinte er:

„Elemente bestehen aus für das jeweilige Element charakteristischen, in sich gleichen und unteilbaren Teilchen, den Atomen“

Im Gegensatz zu den Vorstellungen der griechischen Philosophen unterscheiden sich in seinem Modell die Elemente aber auch durch die Masse und ihr Volumen. Diese Atome können miteinander verbunden und wieder getrennt werden, Atome selbst können jedoch nicht zerstört werden. Bei chemischen Reaktionen ordnen sich demnach die Atome neu an, ändern sich selbst aber nicht. In seinem Modell konnte man allerdings auch noch nicht zwischen einem Atom und einem Molekül unterscheiden.

Dalton versuchte auch eine Ordnung in die Atomgewichte zu bekommen und legte damit einen Grundstein für die spätere Entwicklung des Periodensystems. Auf ihn ist auch Verwendung der Atomaren Masseneinheit (amu oder u) zurückzuführen, die früher mit der Einheit Dalton bezeichnet wurde, und in etwas der Masse eines Wasserstoffatoms entspricht.

 

Thomsonsches Atommodell

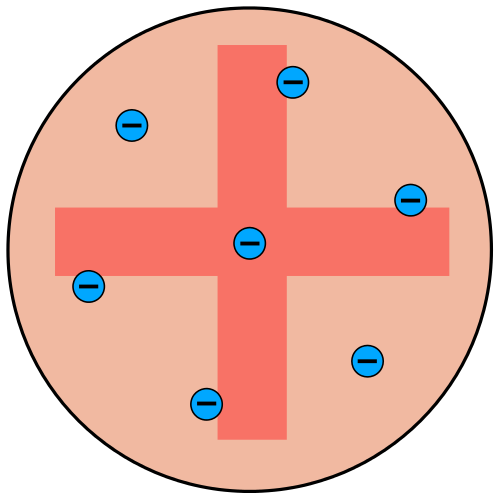
Dieses auch als Rosinenkuchenmodell bekannte Modell wurde 1903 von Joseph Thomson vorgestellt. Wenige Jahre zuvor (1897) wurde als erstes Elementarteilchen überhaupt das Elektron entdeckt und als Bestandteil der Materie ausgemacht. Die angenommene Unteilbarkeit von Atomen war damit Geschichte. Folglich brauchte es ein Atommodell, das die negativ geladenen Elektronen miteinbezieht. In diesem neuen Modell vermutete Thomson die einzelnen Elektronen in einer kontinuierlichen Substanz eingebettet, ähnlich wie die Rosinen im Kuchen verteilt sind. Da das Atom insgesamt elektrisch neutral ist, muss diese Substanz positiv geladen sein und sich mit der Ladung der Elektronen ausgleichen. Thomson vermutete die gesamte Masse des Atoms in den Elektronen konzentriert, wonach der positiv geladene Anteil keine Masse haben sollte. Die Elektronen sind dabei in dieser Masse verteilt und beginnen bei mehr zugeführter Energie zu schwingen.

Bald wurde jedoch bekannt, dass ein Atom gar nicht so viele Elektronen haben kann, dass sich damit die gesamte Masse erklären lässt und man vermutete für Wasserstoff nur ein Elektron. Damit würde aber nur ein Elektron im Wasserstoffatom schwingen. Das Modell erlaubt damit aber nur eine Spektrallinie.

 

-> Was sind Spektrallinien?

Sendet man Licht auf Atome einer bestimmten Sorte, so kann das Licht entweder durchgehen, reflektiert oder absorbiert werden. Wird das Licht absorbiert, so muss die aufgenommene Energie im Atom eine Veränderung bewirken. Im Thomson-Modell äußert sich das durch Schwingungen der Elektronen. Bestrahlt man also ein Atom mit Licht, so werden nur die Frequenzen des Lichts aufgenommen, die das Elektron anregen können und die Elektronen beginnen zu schwingen. Nun stellt man hinter die bestrahlte Materie einen Schirm, der die ankommende Strahlung registriert. In dem ankommenden Spektrum fehlt damit aber genau das Licht, das von den Atomen absorbiert wurde. Das nennt man Absorptionsspektrum. Ein kontinuierliches Lichtspektrum sieht so aus:

 

Ein Absorptionsspektrum sieht dann so aus:

 
Es fehlen darin einige Linien, die genau den aufgenommenen Energien entsprechen und die Elektronen zum Schwingen angeregt haben. Es ist auch möglich, zu beobachten, welches Licht von bestimmten Atomen abgegeben wird, welches nur Licht sein kann, das vorher als Energie im Atom vorhanden war. Ein Atom kann dadurch nur Energien entsprechend seiner Linien abgeben. Sieht man sich dieses Licht, erhält man ein Emissionspektrum, was genau dem umgekehrten Fall eines Absorptionsspektrums entspricht:
 
 
 
Was heißt das nun für das Atommodell?
 
Ein Spektrum wie oben ist wie eine Visitenkarte eines Atoms, denn diese haben alle verschiedene Spektrallinien. Ein Atom gibt mit seinem Spektrum an, welche Energie es aufnehmen kann, also wie die Elektronen angeregt werden können. Ein Atommodell sollte daher nicht nur den Aufbau eines Atoms erklären, sondern auch, warum ein anderes Element ein anderes Spektrum aufweist. Auch zur Zeit Thomsons waren schon einige Spektren von verschiedenen Elementen bekannt.
Thomson war mit seinem Modell aber auf seine schwingenden Elektronen beschränkt. Damit konnte er nicht die verschiedenen Spektrallinien erklären, die in Experimenten auftraten.
 
 
Das Ruthfordsche Atommodell
 
Trotz der fehlenden Erklärung für die Spektrallinien, war das Modell von Thomson das bisher forgeschrittenste Atommodell. 1909 führte jedoch Ruthford ein Experiment durch, das für ein Umdenken sorgte. Wie in nebenstehender Abbildung gab er ein radioaktives Element (1) in eine Bleiabschirmung (2), das die radioaktive Strahlung (3) durch einen Strahl durchlässt. Diese Alpha-Teilchen treffen in einem Punkt (6) auf eine dünne Goldfolie (5). Manche Teilchen werden abgelenkt (7) und treffen auf einen Schirm (4).
Was war nun die Beobachtung?
 
Die meisten Teilchen passierten die Goldfolie ungehindert, einige wurden abgelenkt und manche wurden sogar um mehr als 90° abgelenkt (prallten also in die Gegenrichtung zurück). Aus dem Streuversuch schloss Rutherford, dass sich die Verteilung der Streuung nur dann so ergeben konnte, wenn die positive Masse nicht gleichverteilt im Atom war, sondern sich fest in einem kleinen Punkt, dem Atomkern, konzentrierte. Rechts im Vergleich oben das Thomson-Modell, bei dem die Strahlung ungehindert passieren kann und ein Abprallen nicht sein kann. Im unteren Bild kann Rutherford mit der Annahme eines positiven Atomkerns die Messergebnisse erklären.
 
In dem Atommodell von Rutherford sitzt demnach fast die gesamte Masse im positiven Atomkern, während er von den Elektronen in der Hülle begleitet wird, sodass das Atom insgesamt elektrisch neutral ist. Die Gesamtladung des positiven Atomkerns soll dann genau die Anzahl der Elektronen sein. Wie die Elektronen im Atom verteilt sind, ließ sich aus seinem Experiment jedoch nicht schließen und er ließ diese Frage offen.
Auch wenn sein Modell eine erhebliche Verbesserung gegenüber dem Thomsonmodell hinsichtlich des geometrischen Aufbaus entspricht, war sein Modell nicht in der Lage, die verschiedenen Spektrallinien der Elemente zu erklären.
 
 
Das Bohrsche Atommodell
 
Um die Spektrallinien der Atome erklären zu können, stützte sich Niels Bohr 1913 auf das Modell von Rutherford, führte aber ein, dass die Elektronen den Atomkern auf geschlossenen Bahnen umkreisen. Damit tat sich jedoch ein Problem aus der Elektrodynamik auf: Geladene Teilchen auf einer Kreisbahn strahlen Energie ab. Damit würde ein den Kern umkreisendes Elektron Energie verlieren, also langsamer werden und damit dem Kern näherkommen, bis es in den Kern stürzt. Um dieses Problem zu beheben, verließ Bohr die klassische Mechanik und versuchte Elemente der Quantenmechanik in sein Atommodell einzubauen. Damit war es das erste weithin akzeptierte Atommodell, das durch Postulate die Quantenmechanik beinhaltete. Diese Postulate sind:
 
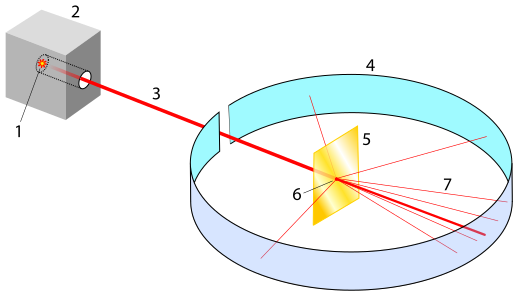
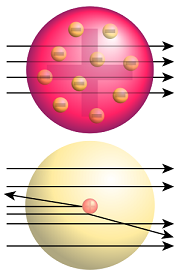
  1. Einem Elektron stehen nicht alle mögliche Bahnen zur Verfügung, sondern nur bestimmte. Auf diesen Bahnen strahlt es keine Energie ab.
  2. Ein Elektron kann von einer Bahn in eine andere Bahn springen. Ein sogenannter Quantensprung kann dann passieren, wenn die Energiedifferenz der beiden Bahnen absorbiert oder emittiert wird.

 

Bohr schafft damit eine kontinuierliche Ansicht ab und schafft die Postulate im klaren Widerspruch zur Elektrodynamik.

Das Bohrsche Atommodell kann im Gegensatz zum Modell von Rutherford u.a. Folgendes erklären:

  • Die Größe eines Atoms kann richtig abgeschätzt werden.
  • Die Spektrallinien des Wasserstoffatoms können nun physikalisch erklärt werden. Die einzelnen fehlenden Linien im Absorptionsspektrum entsprechen der aufgenommenen Energie der Elektronen, die aber nicht zu schwingen beginnen, wie es noch Thomson erklärt hatte, sondern die Energie entspricht einem Quantensprung von einer Bahn auf die andere. Da nur bestimmte Bahnen erlaubt sind, sind auch die Sprünge immer eindeutig in den Spektrallinien zuordenbar.

 

Der Abstand eines Elektrons zum Kern kann im Bohrschen Atommodell gut abgeschätzt werden. Dazu muss man sich vergegenwärtigen, dass beim Kreisen des Elektrons um den Kern einerseits die Coulombkraft, und andererseits die Zentripetalkraft wirkt. Ein Gleichsetzen der Kräfte ergibt

 

 
Um eine Quantenbedingung einzuführen, will Bohr den Drehimpuls des Elektrons quantisieren:
 
 
Umformen auf vn und einsetzen in die erste Gleichung, die dann wiederum auf den Radius r umgeformt wird, liefert
 
 
Für verschiedene n ergeben sich die verschiedenen Radien der Elektronen für das Wasserstoffatom. Damit kann auch die Größe eines Atoms richtig abgeschätzt werden. Errechnet man sich daraus die Energie, kann diese direkt in den Spektrallinien gefunden werden. Bohr konnte damit die Spektrallinien quantitativ mit seinen Rechnungen abgleichen.
 
Dennoch hat auch dieses Modell seine Schwächen:
 
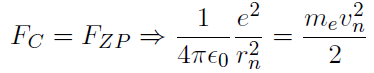
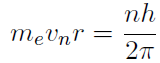
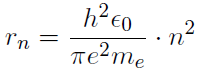
  • Damit wird nur ein Elektron des Wasserstoffatoms beschrieben, mehrere Elektronen gleichzeitig werden nicht berechnet.
  • Das Atom kreist bei Bohr in einer Ebene und damit flach.
  • Chemische Bindungen können mit dem Modell nicht erklärt werden.
  • Nicht alle Linien im Wasserstoffatom können exakt erklärt werden.
  • Es widerspricht nicht nur der Elektrodynamik, sondern auch weiteren Erkenntnissen der Quantenmechanik (z.B. Unschärferelation).

 

Aufgrund seiner hohen Anschaulichkeit wird immer noch oft dieses Modell herangezogen, auch wenn es deutliche Schwächen aufweist.