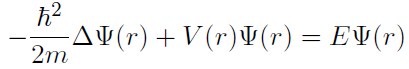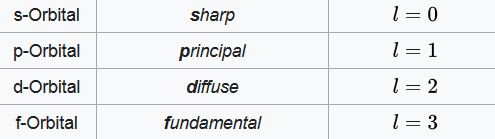Aktuelles Atommodell
Die Grundlagen des bis heute funktionierenden Orbitalmodells stützen sich auf die Schrödinger-Gleichung. Diese Gleichung wurde zwar nicht explizit für die Schaffung eines Atommodells entwickelt und hat eine generelle Gültigkeit, liefert aber ein Atommodell, das mit den experimentellen Ergebnissen übereinstimmt. Die Schrödinger-Gleichung ist ein Postulat der Quantenmechanik und liefert als Differentialgleichung zu einem bestimmten Potential V(r) die Wellenfunktion für ein Teilchen.
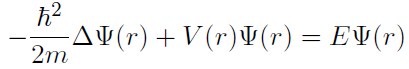
Im Falle des Wasserstoffatoms ist das dafür relevante Potential das Coulombpotential. Die Lösung der Differentialgleichung beschreibt dann das Elektron in Form einer Wellenfunktion. Diese Wellenfunktion gibt an, wie sich das Elektron um den Atomkern herum aufhält, hat aber keine direkte reale Entsprechung, wohl aber ihr Betragsquadrat, denn damit kann man die Aufenthaltwahrscheinlichkeit des Elektrons angeben. Folglich liefert die Schrödinger-Gleichung eine Wahrscheinlichkeitsverteilung über den Aufenthalt des Elektrons. Dieses kugelsymmetrische Problem hat hat auch für das erste Elektron eine kugelsymmetrische Lösung.
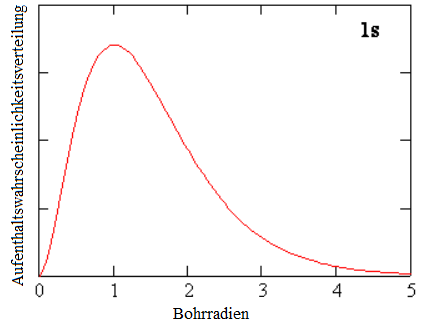
Dem ersten Elektron wird die Hauptquantenzahl n=1 zugewiesen. Dieses Elektron findet man entsprechend der Wahrscheinlichkeitsverteilung rechts im Bild am wahrscheinlichsten einen bestimmten Abstand vom Atomkern entfernt, den Bohr zuvor schon anders ausgerechnet hatte (Bohrradius). Es ist aber durchaus möglich, das Elektron näher beim Kern oder weiter weg anzutreffen. Da diese Kurve kugelsymmetrisch ist, gibt es damit eine kugelschalenähnliche Verdichtung der Wahrscheinlichkeit im Abstand von rund einem Bohrradius.
Wichtig: Das Elektron hat keinen festen Ort, die Wahrscheinlichkeitsverteilung bezieht sich nicht darauf, das Elektron an einem gewissen Ort zu finden, denn das Elektron weiß selbst noch nicht, wo es ist, bis der Ort gemessen wird. Das Elektron legt seinen Ort zum Zeitpunkt der Messung fest und ist zuvor als Welle zu betrachten, die seiner Wellenfunktion entspricht. Die Wahrscheinlichkeit bezieht sich daher nicht auf unsere Unkenntnis eines wohldefinierten Ortes, sondern auf die Unbestimmtheit des Elektrons selbst. Das Elektron kann daher als die Wellenfunktion selbst betrachtet werden, denn es kreist nicht, fährt nicht im Zickzack, noch hat es eine überhaupt eine Bahn im klassischen Sinn um den Atomkern. Die Wellenfunktion des Elektrons bzw. deren räumliche Ausdehnung nennt man Orbital.
Weitere Elektronen, die weitere Orbitale bilden, werden durch weitere Quantenzahlen dargestellt. Die Schrödinger-Gleichung liefert aber nicht nur eine Quantenzahl, sondern mehrere. Orbitale werden daher mit der Hauptquantenzahl n, der Nebenquantenzahl l und der Magnetquantenzahl ml angegeben. Zusätzlich liefert die Gleichung auch mathematische Bedingungen an diese Quantenzahlen:
- l=0,1,2,...,n-1
- ml=-l,-l+1,...,0,...,l-1,l
Außerdem besitzen Elektron einen Spin, der zwei Zustände (Spin up, Spin down) einnehmen kann und miteinbezogen werden muss. Aus anderen Gründen (Pauli-Prinzip) ist es nicht möglich, dass zwei Elektronen den gleichen Zustand einnehmen, d.h. dasselbe Orbital besetzen. Im ersten Orbital (n=1,l=0,ml=0) können daher nur zwei Elektronen sein, denn sie unterscheiden sich im Spin (eines up, eines down). Ein weiteres Elektron kann nicht in dieser Schale Platz finden, sondern muss sich in den Quantenzahlen unterscheiden.
Das nächste Orbital erhält man durch n=2. Laut den Regeln ist dadurch zusätzlich entweder l=0 und ml=0 oder l=1 und ml=-1,0,1 möglich. Dabei hat man sich angewohnt, für die Nebenquantenzahl andere Ausdrücke einzuführen:
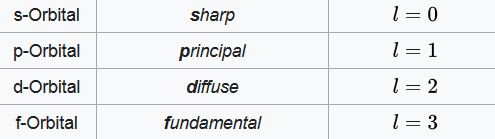
Das allererste Orbital (n=1,l=0,ml=0) ist daher das 1s-Orbital. Das nächste (n=2,l=0,ml=0) das 2s-Orbital. Diese Buchstaben kommen aus der namensgebenden optischen Form, die die Orbitale haben. s-Orbitale sind dabei kugelförmig, p-Orbitale doppelhantelförmig und f-Orbitale rosettenförmig. Die Nebenquantenzahl bestimmt die Form, während die Magnetquantenzahl zusätzlich die Ausrichtung bestimmt. Unten folgt eine optische Übersicht über verschiedene Orbitale.

Im 2s-Orbital (n=2,l=0,ml=0) finden sich wie im 1s-Orbital zwei Elektronen, die sich durch ihren Spin unterscheiden. Im 2p-Orbital jedoch erlaubt die Unterscheidung in die Magnetquantenzahlen mehr Möglichkeiten. So können für jede unterschiedliche Magnetquantenzahl zwei Elektronen, die sich wiederum durch ihren Spin unterscheiden, darin Platz finden, wodurch im 2p-Orbital 6 Elektronen sein können.
Im Gegensatz zum Bohrschen Atommodell ziehen daher die Elektronen nicht auf immer größer werdenden Bahnen ihre Kreise, sondern befinden sich mit gewissen Aufenthaltswahrscheinlichkeiten in räumlichen Bereichen, die die Wellenfunktionen der Elektronen erlauben.
Die Schrödiner-Gleichung ist außerdem auch für mehrere Elektronen gleichzeitig lösbar und ist auch nicht nur auf das Wasserstoffatom beschränkt, sondern kann auf alle Elemente angewendet werden. Die Spektrallinien in einem Spektrum ensprechen den Quantensprüngen zwischen den Orbitalen. Den Spektrallinien kann dadurch genau zugeordnet werden, welche Quantenzahlen dafür verantwortlich sind. Somit ist jedes dieser Spektren eine visualisierte Form der Orbitalsprünge.
Es gibt bisher keine einzige Anwendungssituation, in der dieses Atommodell versagt hätte, deshalb hat dieses 1928 eingeführte Modell bis heute seine Gültigkeit. Durch die komplizierte Mathematik ist es aber schwierig für große Atomkerne mit vielen Elektronen genaue Lösungen zu errechnen, weshalb für alle Elemente außer dem Wasserstoff Näherungen gemacht werden müssen. Die sichere Bestimmung von Spektrallinien ist mittlerweile keine Frage des passenden Modells mehr, sondern eine Frage der geschickten Näherungen und vorhandener Rechenkapazität.
Was kann das Orbitalmodell noch?
Für jegliche Art von Potentialen kann die Schrödinger-Gleichung Wellenfunktionen liefern, die die Elektronen beschreiben. Daher ist es auch möglich, Moleküle damit zu beschreiben und je nach chemischen Bindungen lassen sich dadurch auch Molekülorbitale beschreiben. Die anfangs präsentierte Gleichung ist außerdem nicht nur als zeitunabhängige Gleichung brauchbar, sondern es gibt auch eine zeitabhängige Version, mit der sich zeitlich verändernde Vorgänge, z.B. ein Bindungsvorgang oder das Auftrennen einer chemischen Bindung zeitlich beschrieben werden können.
Da sich die kinetischen Energien der Elektronen durchaus in Größenordnungen bewegen, die einen Einbezug der speziellen Relativitätstheorie sinnvoll machen, existeren zusätzlich auch relativistischen Korrekturen für die Schrödinger-Gleichung. Eine weitere Verfeinerung des Modells ist durch die Quantenelektrodynamik gegeben, die auch das elektrische Feld quantisiert betrachet und daher noch genauere Lösungen für spezifische Situationen zulässt.